7.4 Hierarchical k-means clustering
Based on industrial experience, it is known that outputs of higher importance have a greater influence on defining production routes. To reflect this, we explored hierarchical k-means clustering, i.e., performing k-means clustering in a hierarchical manner based on the importance of each output. The process is as follows:
1. Apply k-means clustering to all output data X, with initialized centroids, to create two clusters. Record the resulting cluster centroids.
2. Data from the first cluster is excluded from further clustering. Apply the same k-means clustering method to the data from the second cluster to create two new clusters, and record the resulting centroids.
3. Repeat step 2 until the number of clusters reaches k or only one member remains and cannot be further clustered.
4. During prediction, each data point Yi is initially evaluated for its proximity to the centroids of the first-level clusters. If Yi is assigned to a cluster at this level, the assignment is recorded. Otherwise, the distances between Yi and the centroids at the subsequent level are computed to determine whether Yi belongs to a cluster at the current level or if the evaluation should proceed to the next level. This process continues until the cluster assignment for Yi is definitively established.
SPL routine:
| A | B | C | D | ||
|---|---|---|---|---|---|
| 1 | [[0.113,0.345,0.316], [0.118,0.314,0.322], [0.125,0.334,0.314], [0.139,0.254,0.371], 0.111,0.361,0.306], [0.179,0.257,0.332]] |
/X | |||
| 2 | [[0.116,0.371,0.307], [0.143,0.324,0.303]] |
/Y | |||
| 3 | =mk=3 | ||||
| 4 | =center_seq=[] | ||||
| 5 | =xc=A1.(0) | ||||
| 6 | =idx_seq=to(A1.len()) | ||||
| 7 | =col_seq=to(A1.~.len()) | ||||
| 8 | =mstd@s(A1,1).~ | ||||
| 9 | for | =A1(idx_seq) | /Remaining data | ||
| 10 | =transpose(B9)(col_seq) | ||||
| 11 | =A8(col_seq).psort@z() | /Sidx | |||
| 12 | =B10(B11) | ||||
| 13 | =B12.(~.ranks()) | /Transpose of RK | |||
| 14 | =as=to(B13.len()),av_idx=to(B9.len()),B13.((oidx=as#,pma=(~–msum(B13(oidx),1).~)(av_idx).pmax(),res=av_idx(pma),av_idx.delete(pma),res)) | /Cb index | |||
| 15 | =B9(B14.select(~)) | /Cb’ | |||
| 16 | =B15.to(2) | /Initialized centroids C | |||
| 17 | =k_means(B9,2,300,B16) | ||||
| 18 | =B17(1) | ||||
| 19 | =B17(2) | ||||
| 20 | =B19.run(~=~+A9-1) | ||||
| 21 | =B20.group@p(~) | ||||
| 22 | =B21(1) | ||||
| 23 | =B21(2) | ||||
| 24 | =idx_seq(B22) | ||||
| 25 | =idx_seq(B23) | ||||
| 26 | =xc(B24)=B20(B22) | ||||
| 27 | =idx_seq=B25 | ||||
| 28 | =col_seq(B11.~) | ||||
| 29 | =col_seq=col_seq\B28 | ||||
| 30 | =center_seq.insert(0,[B18]) | ||||
| 31 | if idx_seq.len()==1||A9==mk-1 | =xc(B25)=B20(B23) | |||
| 32 | break | ||||
| 33 | =center_seq | /Set of centroids | |||
| 34 | =yc=[] | ||||
| 35 | =A33.len() | ||||
| 36 | for A2 | for A33 | =B36.pmin(dis(~,A36)) | ||
| 37 | =#B36 | ||||
| 38 | =C36+C37-1 | ||||
| 39 | if C36==1||C37==A35 | =A34.insert(0,C38) | |||
| 40 | next A36 | ||||
| 41 | return [center_seq,xc,yc] | ||||
Calculation result example:
Yield data X:
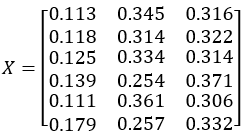
Number of clusters k=3
Prediction data Y:

First-level centroids, C1:

Second-level centroids, C2:

Cluster assignments for members in X, Xc:
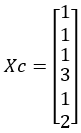
Cluster assignments for members in Y, Yc:
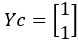
The routine contains a relatively small amount of data. After the second level of clustering, only a single data point remains, making further hierarchical division impossible. Consequently, even if the number of clusters k is increased to 4 or more, the clustering will still only yield 3 clusters. This limitation is inherent to the hierarchical k-means algorithm. Therefore, when clustering into a specific, predetermined number of clusters is required, the k-means algorithm with initialized centroids, as introduced earlier, should still be used.
SPL Official Website 👉 https://www.esproc.com
SPL Feedback and Help 👉 https://www.reddit.com/r/esProcSPL
SPL Learning Material 👉 https://c.esproc.com
SPL Source Code and Package 👉 https://github.com/SPLWare/esProc
Discord 👉 https://discord.gg/sxd59A8F2W
Youtube 👉 https://www.youtube.com/@esProc_SPL


