The goal of industrial production is to transform raw materials into products, thereby generating profit. Raw materials undergo a series of processes – including physical and chemical reactions – to ultimately yield the desired products. Ideally, the conversion rate from raw materials to products is fixed, allowing factories to precisely calculate the required raw material quantities for target production volumes, thereby improving efficiency.

In industry, raw materials are referred to as ‘inputs’ and products as ‘outputs’. Many process principles and practical experience suggest that, under simplified conditions, a linear relationship can often be assumed between input quantities and output quantities. This implies a constant conversion rate – known as the yield – between each input and output, independent of the input quantity. Industrial production environments impose the following constraints on these yield rates:

Constraint 1: The yield of any output from any input must be within the range of [0, 1]. This ensures that we cannot produce more output than we input, and that no output has a negative yield.

Constraint 2: Mass conservation. Any input is ultimately converted into various outputs; no input is left unused, and no output is created from nothing. Therefore, the sum of yields from a single input to all outputs must equal 1.

Constraint 3: Industrial knowledge provides baseline yields. While these values may not be precise, actual yields cannot deviate significantly from them. Furthermore, if a baseline yield is zero, the corresponding actual yield must also be zero.

Describe in mathematical language:

Let the matrix X represent inputs, Y represent outputs, and W represent yields.

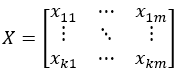
Where k is the number of samples and m is the number of inputs, x_ij is the j-th input for the i-th sample, X_ri represents all inputs for the i-th sample, and X_cj is the j-th input across all samples.

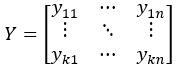
Where n is the number of outputs, y_ij is the j-th output of the i-th sample, Yr_i is all outputs of the i-th sample, and Yc_j is the j-th output of all samples.

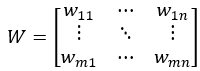
Where w_ij is the yield from the i-th input to the j-th output, W_ri is all yields for the i-th input, and W_cj is all yields for the j-th output.

The constraints that W needs to satisfy are as follows:

Constraint 1: w_ij ∈[0,1]

Constraint 2: sum(Wr_i)=1

Constraint 3: Baseline yields are denoted by B.

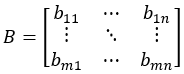
if(b_ij==0,w_ij=0, |w_ij-b_ij|<ε)

Where ε is a relatively small number, and B itself satisfies constraint 2, and sum(Br_i)=1.