6.3 Calculating boundaries using the error limitation method
To satisfy Constraint 3 (yield cannot deviate too far from baseline yield), the difference between a yield and its baseline yield is called “deviation yield,” denoted as WE.
WE=W-B
With the yield W constrained to [0,1] and a fixed baseline yield B, the theoretical range of the deviation yield WE is [-1,1]. However, this range is too broad. Because inputs and outputs are adjusted daily in production, we aim for today’s yield to closely approximate yesterday’s. When calculating the deviation yield boundary range, we can consider the input-to-output conversion rate of the last day (row) as a benchmark. Using this benchmark and the baseline yield, we can calculate the deviation yield boundary BD. We call this method the “Error Limitation Method.” The calculation process is as follows:
Assume the deviation yield boundary BD has the following form:
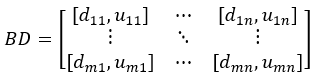
Where dij represents the lower bound of the deviation yield for the i-th input and j-th output, while uij represents the upper bound.
The last row of input and output data:
Xrm=[xm1,xm2,…,xmn]
Yrm=[ym1,ym2,…,ymn]
(1) Calculate theoretical output, YTrm:
YTrm=Xrm*B
(2) Calculate the difference (DFrm) between theoretical and actual output:
DFrm=Yrm-YTrm
(3) Calculate the ratio of DFrm to total input (Prm)
Prm=DFrm/sum(Xrm)
(4) Calculate the deviation yield boundary BD:
Set a proportion for the BD’s allowable adjustment, denoted as pg.
The reference adjustment values d’mj and u’mj for BD are calculated based on Prm and pg, as follows:
d’mj=if(pmj>0,pmj*(1-pg),pmj*(1+pg))
u’mj=if(pmj>0,(pmj*(1+pg),pmj*(1-pg))
Where pmj is the j-th element of Prm.
Originally, this boundary could be used for the deviation yields of all corresponding inputs. However, we need to ensure that all yields are within the range of [0,1] and that when the baseline yield is 0, the yield is also 0, and the boundary upper and lower limits must also be 0.
dij and mij must satisfy the following four inequalities:
dij+bij ≥0
uij+bij ≥0
dij+bij ≤1
uij+bij ≤1
Calculate BD using the inequalities and the baseline yield B:
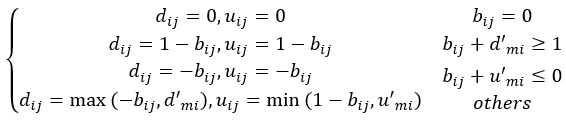
SPL routine:
| A | B | |
|---|---|---|
| 1 | [[30,8],[31,7],[38,10]] | /X |
| 2 | [[2,13,23],[3,15,20],[11,13,24]] | /Y |
| 3 | [[0,0.5,0.5],[0.55,0.05,0.4]] | /B |
| 4 | 0.1 | /rg |
| 5 | =A1.m(-1).sum() | /Total Xrm |
| 6 | =mul([A1.m(-1)],A3).~ | /Theoretical output, YTrm |
| 7 | =A2.m(-1)–A6 | /Difference between actual and theoretical output, DFrm |
| 8 | =A7.(~/A5) | /Ratio of DFrm to total Xrm, Prm |
| 9 | =A8.([if(~>0,~*(1-A4),~*(1+A4)),if(~>0,~*(1+A4),~*(1-A4))]) | /D’rm,U’rm |
| 10 | =A3.(~.((r=A9(#),(if(~==0,[0,0],if(~+r(1)>1,[1-~,1-~],if(~+r(2)<0,[-~,-~],[max(-~,r(1)),min(1-~,r(2))]))))))) | /Deviation yield boundary BD |
Calculation result example:
Input X:
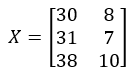
Output Y:
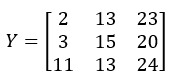
Baseline yield B:
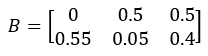
Boundary adjustment ratio rg:
rg=0.1
Calculated boundary BD:
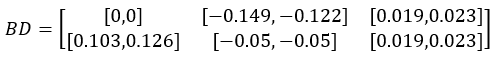
SPL Official Website 👉 https://www.esproc.com
SPL Feedback and Help 👉 https://www.reddit.com/r/esProcSPL
SPL Learning Material 👉 https://c.esproc.com
SPL Source Code and Package 👉 https://github.com/SPLWare/esProc
Discord 👉 https://discord.gg/sxd59A8F2W
Youtube 👉 https://www.youtube.com/@esProc_SPL


