Derived sequences such as original values, rate of change, and dispersion can all be used to detect anomalies, yielding corresponding alarm intensity sequences. These alarm intensity sequences are then composited in some way to represent the overall alarm intensity, which is called the ‘composite alarm intensity’, denoted Wns.

Whether using original values or any other derived sequence to calculate anomaly scores, most values fall within the range of [0,1]. Alarm intensity, being a moving weighted average of anomaly scores, also predominantly falls within [0,1], ensuring consistent units. Therefore, the simplest approach when dealing with multiple alarm intensity sequences is to calculate a weighted average to obtain the composite alarm intensity Wns.

Assume there are p alarm intensity sequences, which form an alarm intensity matrix WnM:

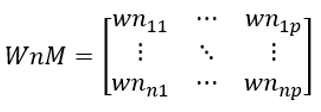
where wn_ij is the alarm intensity of the j-th alarm sequence at i-th time point. Each row of WnM represents the set of alarm intensities at a given time point, and each column represents an alarm intensity sequence.

Assuming the weight of each alarm intensity sequence is Wh, the composite alarm intensity is calculated as the weighted sum of the alarm intensities at every time point.

Wh=[wh₁,wh₂,…,wh_p]

sum(Wh)=1

Wns_i=sum([wn_i1,wn_i2,…,wn_ip]**Wh)

where Wh_j is the weight of the j-th alarm intensity sequence.